To see the greatest return on investing in genomic-enhanced EPDs, cattle breeders must decrease the average age of sires and dams. The factors which determine genetic change are straightforward and can be expressed in mathematical terms by the following equation:
?G = [r * sg* i ] / L
where:
?G = the change per year in the trait’s genetic merit within the population.
r = the accuracy of the selection.
sg = the amount of genetic variation present in the population.
i = the selection intensity.
L = the generation interval (the average age of a calf’s parents on the day of its birth).
The accuracy of selection (r) is the correlation between the true breeding value and the estimate used for selection decisions. When observed measurements, such as actual weaning weight, are used to make selection decisions, r is the square root of the heritability (i.e., the portion of variation in the trait due to genetics). When EPDs are used for selection, the accuracy of the EPD determines r. The accuracy of selection using EPDs is always larger than the accuracy from using observed measurements (i.e., phenotypes).
The genetic variability of the trait within the population is measured by the standard deviation (sg). The genetic standard deviation measures how much observations range around the average. If most animals are close to average, the standard deviation is small. If there is more variation and animals are not as close to average, the standard deviation is larger. In terms of the response to selection (?G) the amount of genetic variability is the one component that breeders do not typically control.
The selection intensity measures how different the selected parents are from the overall population average. If the selected parents are close to the population average, the selection intensity is small. If the parents are quite different from the population average, the selection intensity is large. In other words, the selection intensity reflects whether the parents are from the top 25%, 5%, 1%, etc. of the population (i.e., percentile rank).
The focus of this fact sheet is changing the generation interval. The generation interval is the average age of parents when the next generation is born. If older bulls and cows are used as parents, the generation interval is longer and genetic change is slower. But if we use younger bulls and cows and replace older generations with younger generations, the generation interval is shorter and genetic progress is more rapid. From the equation presented earlier, L is in the denominator and thus can have a large impact on the amount of genetic progress that can be made.
Effect of decreasing generation interval
Let’s look at some historical data to get a feel for the relationships between selection accuracy, selection intensity and generation interval. From a study analyzing 3,570 Angus animals, the rate of genetic change for weaning weight was estimated as 2.8 pounds per year, the genetic standard deviation for weaning weight was 26.3 pounds, and the generation interval was 5 years. These values lead to accuracy multiplied by intensity equaling 0.53 (r * i=0.53). If we assume true accuracy is 0.5 (equal to a BIF accuracy of 0.13), then intensity is 1.07.
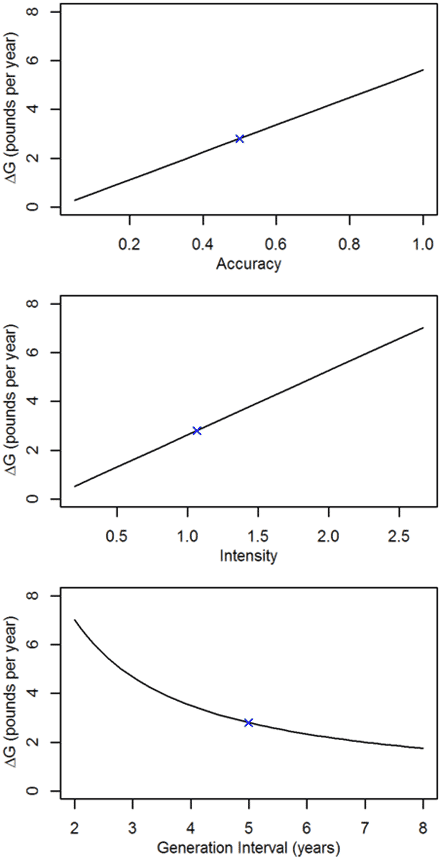
We can vary the values of accuracy, intensity and generation interval and observe the results on genetic change. These graphs depict that increasing accuracy by 20% results in a 16.7% increase is genetic change; accuracy has the smallest effect on genetic change. Increasing intensity by 20% results in a 20% increase in genetic change. (The slope of the lines in the top two panels of Figure 1 are not the same.) But by decreasing generation interval by 20% (5 years to 4 years) we see a 25% increase in genetic change. Further, unlike the relationship between ?G and r or i, the relationship between ?G and L is not a straight line; ?G increases more rapidly as we decrease L. If we decrease generation interval from 5 years to 3.5 years, genetic change increases by 43%. Thus, because generation interval is the lone term in the denominator of the genetic change equation, it has the largest impact on genetic change per year.
But, historically, accuracy and generation interval were not independent. To increase accuracy we needed older bulls with more progeny records, thus generation interval increased. To decrease generation interval we used younger bulls with less data and lower accuracy. As discussed in the next section, genomic-enhanced EPDs can help alleviate this negative relationship. If we have a 20% decrease in accuracy resulting from a 20% decrease in generation interval, genetic change remains the same. But younger bulls can often have superior genetic merit compared to older bulls, thus using young bulls increases the selection intensity.
Strategies to decrease generation interval
What are some strategies we can use to increase genetic progress by decreasing generation interval while balancing accuracy and intensity? The bull side of the equation has the easiest identified solutions. We often see beef producers use proven bulls that are 10 or 15 years old in artificial insemination programs. While this may be a useful practice in the commercial industry where increased EPD accuracy provides confidence particularly for traits like calving ease, it is not advantageous in the seedstock sector. Seedstock breeders benefit from using younger sires, and they can offset some of the risk in using lower accuracy sires by using more sires. The dairy and swine industries have successfully employed the practice of using a larger number of young sires. This practice has several advantages. First, using young sires shortens the generation interval and increases genetic progress, as we have previously discussed. Second, young sires take advantage of the genetic trend of a breed, thus they are more likely to rank higher for the economically important traits that are under selection compared to older sires. Third, new developments in genomic testing have increased the accuracy of young sire EPDs. While historically interim EPD accuracies of young bulls have been around 0.1, genomically-enhanced EPD accuracies are closer to 0.4 depending upon the trait of interest. Fourth, by using a larger number of sires, producers can hedge against unfavorable changes in EPD estimates. As the EPD estimates for the selected young sires become more accurate with additional new data, some sire’s EPDs will worsen whereas the EPDs of other sires will improve. The progeny of the under-performing sire can be sold as feeder calves or commercial replacement females, and the producer will reap the benefits of the sire’s progeny that outperformed his previous EPD estimate. For example, a producer selects a group of bulls that rank in the 15th percentile for an economic selection index. As newly collected data are used in EPD estimation in the following years, some sires will stay near the 15th percentile, some will drop to the 25th percentile and some will rise to the 5th percentile. As a consequence, the average of the bull battery stays intact, and in fact the accuracy of the mean of the group is larger than the accuracy of any one sire. The producer can chose to sell the progeny of bulls that fell to the 25th percentile. But, the producer now has progeny sired by a bull in the 5th percentile, i.e., thus the bull performed better than expected.
Strategies to decrease the generation interval on the female side of the equation may be cost prohibitive. It often takes 5 to 6 years of production for a producer to break even on the investment in a cow in a commercial operation (see the Replacement Cow Bid Price Calculator to estimate prices and break even year for your situation). But the seedstock sector may have opportunities to shorten the generation interval in females. One approach may be to use younger females in embryo transfer programs. With a genomic prediction, cows can have the same accuracy behind their EPDs as if they had 10 to 20 progeny records. These more reliable EPD estimates may allow producers to use younger cows as embryo donors. This approach will not be as dramatic as using younger sires.
Conclusion
When a systematic approach is taken to decrease generation interval by balancing accuracy and intensity, more rapid genetic change can be achieved. The largest gains in accuracy from genomic predictions are seen in young animals with little performance data behind their EPD estimates. By using these young animals as parents we take advantage of the investment in genomic testing, but we also shorten the generation interval. By using a larger number of sires with genomic-enhanced EPDs we can take advantage of the increased genetic progress resulting from a shorter generation interval.